|
||||||
|
|||||||
Kot je opisano v prejšnjem poglavju, na fotone deluje sila gravitacije. Eddigton
je leta 1919 izmeril, da foton, ki leti mimo Sonca, spremeni smer svoje poti,
zaradi gravitacijske privlačnosti Sonca.
Foton mora torej s silo na neki poti premagovati gravitacijsko polje, kadar
želi pobegniti iz nekega nebesnega telesa. Pojav je še posebej opazen v primeru
črnih lukenj, ko foton praviloma velike gravitacije, z energijo, ki jo premore,
ne more premagati.
Ko foton premaguje gravitacijsko polje, izgublja del lastne energije. Na foton
deluje zaviralna sila na njegovi poti.
Vpliv energijskih izgub na grozd fotonov
Tega siromašenja energije na nivoju fotonov z meritvami praviloma ne zaznamo.
Meritve kažejo vedno enake energije fotonov izbranih frekvenc.
Pojav velike energijske stabilnosti fotonov si lahko razlagam na osnovi izmenjave
energije med fotoni, kot je opisano v poglavju Foton, ter sprotnemu prilagajanju
števila fotonov aktualni energiji fotonskega grozda.
Ob energijskih izgubah se zmanjšuje število fotonov znotraj grozda zato, da
fotoni lahko ohranjajo optimalno energijo.
Pobeg fotona iz črne luknje
V nadaljevanju si podrobneje ogledam poskus pobega fotona iz črne luknje. Črne
luknje praviloma ne oddajajo svetlobe, kar pomeni, da iz črne luknje foton ne
more pobegniti.
V črni luknji je učinek gravitacijske privlačnosti zelo velik. Črna luknja tako močno privlači fotone, da le-ti ne morejo pobegniti iz nje.
Fotoni v naši okolici imajo enako energijo.
Grozd fotonov zaradi privlačne sile na poti pobega iz nebesnega telesa z veliko
gravitacijo izgublja svojo energijo. Na poti premaguje privlačno silo.
Energija grozda fotonov se v primeru premagovanja gravitacije spreminja zvezno,
skladno z enačbo A = F.s. Izgubljena energija fotonskega grozda je produkt privlačne
sile na foton in opravljene poti.
Grozd fotonov na poti posledično postaja energijsko osiromašen. Ko se pojavi
določen energijski primanjkljaj v grozdu fotonov, se grozd odpove enemu od svojih
fotonov. Število fotonov v grozdu se zmanjša za en foton, kot to prikazuje slika
3.19 (Foton).
Ko energija fotonov v grozdu dovolj pade, se zmanjša število fotonov v grozdu za en foton. Grozd zgubi enega od svojih fotonov. Takrat se pojavi energijska obogatitev ostalih fotonov grozda, ki pa z nadaljnjim dviganjem v gravitacijskem polju naprej izgubljajo energijo, kot prikazuje slika 7.2.
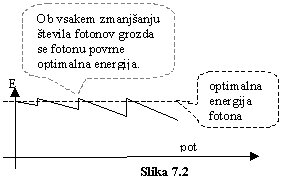
Če je grozd fotonov številčno bogat, potem odstranitev posameznega fotona zanemarljivo
vpliva na energijo ostalih fotonov. Na sliki 7.2 je posledično prvi skok spremembe
energije na začetku poti energijsko neznaten.
Kadar pa se v grozdu fotonov znajde le še nekaj fotonov, takrat zmanjšanje
števila fotonov v takem grozdu pomeni prehod iz precejšnje energijske siromašnosti
v precejšnjo energijsko bogatost preostalega fotona, kot prikazuje zadnji skok
energije fotona na sliki 7.2.
Ob prehodu dveh fotonov v enega, ko edini preostali foton prevzame energijo
obeh fotonov, je skok energije največji.
Osamljeni fotoni
Ko se grozd fotonov zmanjša na en foton, takrat je konec energijske solidarnosti
med fotoni. Foton ostane sam.
Tudi tak foton še naprej premaguje gravitacijsko polje in še naprej energijsko
slabi.
V izbranih razmerah lahko torej pričakujemo tudi posamezne energijsko osiromašene
fotone. Takšni fotoni so dokaj neopazni, saj se pojavljajo le v redkih izjemnih
okoliščinah, so osamljeni, in pa energijsko revni.
Za ilustracijo naj navedem, da človeško oko takih, energijsko osiromašenih
fotonov ni sposobno zaznati. Spodnja meja je zaznavanje enega energijsko ne
osiromašenega fotona. Kadar pa človeško oko želi zaznavati barve, pa je potrebnih
vsaj sto fotonov, ki v grozdu zadenejo barvni stožec na ozadju očesa.
Radijsko valovanje in foton
V poglavju foton je opisano, da radijska valovanja in foton sestavljajo EM
valovi, ki jih opisujeta isti Maxwellovi enačbi.
Radijsko valovanje praviloma zaznavamo kot energijsko ne optimalno, kot energijsko
preveč bogato. Fotone opažamo kot energijsko optimalno valovanje.
Seveda tudi radijski valovi lahko postanejo energijsko optimalni, skladno s
Plackovim zakonom. Ravno tako, čeprav tega pogosto ne opažamo, fotoni lahko
postanejo energijsko revni, z manj energije, kot jo fotonom pripisuje Planck,
kadar fotoni na poti energijo zgubijo in nimajo možnosti izmenjati energije
z drugimi fotoni.
Ni poznane meritve za merjenje osiromašenih fotonov
Energijo fotonov merimo praviloma na osnovi energijskega učinka, ki ga ima
foton na ponoru. Merimo na primer, kdaj nek foton lahko izbije elektron iz krožnice
atoma, kot to prikazuje slika 4.2 v poglavju Antienergija. Ker poznamo vezalno
energijo takega elektrona v krožnici, iz te energije lahko sklepamo na energijo
vpadnega fotona.
Ta metoda pa ne omogoča merjenja energije morebitnih osameljenih fotonov z
manjšo energijo, ki bi bili pomešani med fotone z optimalno energijo.
Metoda merjenja energije fotonov na osnovi izbijanja elektronov iz krožnice
atoma nam zagotavlja, da ima foton neko optimalno energijo, ki je odvisna od
frekvence fotona. Zagotavlja nam, da imajo fotoni v večini primerov takšno energijo,
kot ugotavlja Planck - E=f.h.
Ta metoda merjenja energije fotona pa ne daje odgovora, ali obstajajo med opaženimi
fotoni tudi energijsko siromašni fotoni.
Metoda merjenja energijsko siromašnih fotonov
Pred znanostjo je torej izziv, da z meritvami dokaže ali ovrže obstoj energijsko
siromašnih fotonov. Meritev bi lahko temeljila na ugotovljenem dejstvu, da foton,
ki zadane v elektron nanj deluje s silo. Foton ne deluje s silo le na vezane
fotone ampak tudi na svobodne fotone.
Merilni instrument bi bila lahko katodna cev, skozi katero tečejo elektroni,
podobno kot v televizijskem sprejemniku. Zagotoviti bi morali gibanje vseh elektronov
z enako in znano hitrostjo. Obstreljevanje elektronov s fotoni s strani, pod
kotom devetdeset stopinj, bi povzročilo večji ali manjši odklon elektronov v
katodni cevi, odvisno od energije fotonov. Odklon bi bilo lahko merilo o energiji,
fotona, ki zadane v elektron.
Dokler z meritvijo ne dokažemo obstoja ali ne obstoja fotonov različnih energij,
do takrat nobene možnosti ne smemo izključiti. Dopuščati moramo možnost obstoja
tudi energijsko siromašnih fotonov.
Energijsko siromašni foton
Osamljen foton lahko premaga gravitacijsko polje nekega telesa, kadar izhaja
iz nebesnega telesa z manjšo gravitacijo.
Kadar grozd fotonov izhaja iz nebesnih teles z veliko gravitacijo, kadar se
masa nebesnega telesa približuje masi črne luknje, foton le s težavo premaga
gravitacijsko polje.
Kadar pa grozd fotonov izhaja iz črne luknje, grozd s premagovanjem sile na
poti postaja vse manj številčen (slika 7.2), nakar ostane osamljen foton.
Tudi ta preostali osamljen foton gravitacije črne luknje ne more premagati.
Lastna energija fotonu ne zadošča za pobeg in osvoboditev iz črne luknje.
Planck je torej opazil le fotone optimalnih energij.
Planck je v primeru svetlobnega valovanja prišel do navidezno drugačne ugotovitve.
Planck trdi, da ima svetloba določene frekvence vedno enako energijo. Energija
fotona po Plancku je enaka:
E = f. h.
Planckova trditev pomeni, da ima elektromagnetno valovanje fotona določene
frekvence vedno enako amplitudo.
Zaradi združevanja fotonov v grozde, kot prikazuje slika 3.19 v poglavju 'Foton'
in energijske solidarnosti med fotoni, so energijsko revni fotoni zelo redki.
Zaradi njihove redkosti in za take meritve neprimernih merilnih metod, jih ne
moremo opaziti.
Razmerje med valovno dolžino in amplitudo fotona je le na
izvoru svetlobe vedno enaka.
Iz Plankovih meritev lahko sklepam, da je razmerje med valovno dolžino (frekvenco)
in energijo (fotona) na izvoru, vedno v razmerju, ki ga določa enačba E=f.h.
Kaj se dogaja z osamljenim fotonom ob energijskih izgubah fotona, lahko sklepamo
na osnovi Maxwellovih enačb, ki pravijo, da se energija elektromagnetnega vala
(fotona) po nastanku lahko spreminja tudi ob nespremenjeni frekvenci.
Foton na poti iz črne luknje izgublja lastno energijo.
V nadaljevanju se osredotočim na energijsko dogajanje posameznega fotona. To
je dogajanja od takrat naprej, ko foton zaradi energijskih izgub ostane sam,
brez ostalih fotonov v grozdu.
Za premagovanje privlačne sile na poti iz črne luknje osamljeni foton rabi
energijo. Za vsak nadaljnji kilometer poti, ki jo foton napravi ob dvigovanju
pri poskusu pobega iz črne luknje, porabi del svoje notranje energije.
Foton takrat, ko ostane sam brez solidarnosti v grozd povezanih fotonov, na
neki višini iz črne luknje, razpolaga v tistem trenutku z neko lastno energijo.
Ta energija mu služi za premagovanje gravitacijske sile ob nadaljnjem dviganju
iz črne luknje.
Z dvigovanjem fotona v gravitacijskem polju se mu zmanjšuje njegova notranja (valovna) energija, povečuje pa se mu potencialna energija.
Notranja energija fotona se pretvarja v njegovo potencialno energijo.
Črna luknje in aktivna galaktična središča
Galaksije v svojem središču vsebujejo bodisi črno luknjo bodisi aktivno galaktično
središče. Kadar je masa jedra galaksije tako velika, da ne dovoljuje svetlobi
pobega iz jedra galaksije, potem tako jedro galaksije imenujemo črna luknja.
V primerih, ko je središče galaksije manj masivno in galaktično središče izsevanih
fotonov ne more zadržati, tako središče galaksije imenujemo aktivno galaktično
središče.
Med znanstveniki o aktivnih galaktičnih jedrih obstaja tudi drugačno mnenje,
temelječe predvsem na ugotovitvah Edwina P. Hubble, opisanem v nadaljevanju.
Oddaljenost in hitrost galaksij
Edwin Hubble je opazoval spektre vidne svetlobe več bližnjih galaksij. V vidni
svetlobi je opazil spremembe valovnih dolžin (spektralnih črt), značilnih za
posamezne tipe atomov (vodik). Spremembe valovnih dolžin je povezal z radialnimi
gibanji galaksij glede na nas.
Edwin Hubble je leta 1929 izmeril hitrost 18 bližnjih galaksij. Ugotovil je,
da se galaksije praviloma oddaljujejo od nas. Ko je primerjal njihovo oddaljenost
in hitrost, je ugotovil, da je hitrost oddaljevanja galaksije sorazmerna z oddaljenostjo.
Na nebu je precej galaksij z velikim rdečim premikom.
Na nebu opažamo galaksije, kjer ima iz njih izhajajoča svetloba dvojno valovno
dolžino. Foton, ki ima v tipičnem spektru vodika valovno dolžino 486 nm, do
Zemlje prispe s še enkrat večjo valovno dolžino. Namesto modrega fotona na izvoru
(486 nm) na Zemlji opazimo prihod infrardečega fotona z valovno dolžino 972
nm.
Največji rdeči premiki so večji od ena. Trenutni rekord ima galaksija z rdečim
premikom 5,1.
Značilno za galaksije z velikim rdečim premikom so zelo svetla aktivna središča.
Leta 1994 je Hubblov teleskop omogočil razkrivanje galaksije M87, kot prikazuje
slika 7.4.
Paradoks galaksije M87
Če bi dogajanje na galaksiji M87 ocenili le na osnovi Hubblovega zakona, bi
dobili nesmiselne rezultate.
Hubblov zakon kaže, da plin okrog galaksije M87 kroži s hitrostjo 550 km/s, mnogo večjo hitrostjo od krožilnih hitrosti zvezd v kateri koli galaksiji.
Na osnovi Newtonovega gravitacijskega zakona bi lahko sklepali, da bi moralo biti v galaksije M87 črna luknja z maso 3 milijard naših Sonc.
Rezultat je popolnoma izven pričakovanj.
Če nadaljujem, lahko ugotovim, da bi curki snovi, ki se širijo od središča
galaksije M87 navzven, morali imeti skoraj svetlobno hitrost.
Ni razlage in pojasnila, kako naj bi delec pobegnil grozljivo močni gravitaciji
galaksije M87 s svetlobno hitrostjo.
Četudi bi delec na izvoru na površini aktivnega galaktičnega središča imel
svetlobno hitrost, bi mu močna gravitacija kaj kmalu izničila še tako veliko
hitrost.
Hubblov zakon torej ne more biti edina osnova za pojasnjevanje aktivnih galaktičnih
jeder. Obstajati mora torej neka bolj verjetna in utemeljena razlaga za opis
opaženih dejstev na galaksiji M87.
Vpliv gravitacije na frekvenco fotona.
Ljudje živimo in opazujemo okolico v razmerah majhnih gravitacijskih polj.
Zakonitosti svetlobe, ki jih merimo, veljajo torej za okolja, kjer so gravitacijska
polja majhna.
V bližini črnih lukenj, oziroma v bližini aktivnih galaktičnih središč nastopajo
zelo močna gravitacijska polja, v katerih se rojevajo fotoni.
Kadar se fotoni rojevajo v razmerah velike gravitacije, močna gravitacijska
polja lahko vplivajo na lastnosti fotonov. Močna gravitacija lahko vpliva na
oblika in velikost posameznega fotona. Nastali fotoni imajo lahko drugačno razmerje
med energijo in frekvenco.
Rdeči premik je lahko posledica rojevanja fotonov v okoliščinah
velike gravitacije.
V primeru aktivnih galaktičnih jeder je opažen rdeči premik lahko posledica
delovanja ne le ene, ampak dveh zakonitosti: Na primer:
· Del rdečega premika (zmanjšanja frekvence fotona) lahko pripišemo hitrosti
in oddaljenosti aktivnega galaktičnega jedra skladno z Hubblovim zakonom.
· Del rdečega premika lahko pripišemo nastanku fotona v močnem gravitacijskem
polju galaktičnega središča.
Vpliv 'zakrivljenosti prostora' na frekvenco fotona.
V okolju, kjer zanemarim učinke gravitacije, frekvenco fotona določa enačba f = c/l.
---------------------------------------------------------------
- Tomaz Zwitter: Pot skozi vesolje, Modrijan zalozba, Ljubljana
2002
- F. Shu: The Physical Unverse, University Science Books, 1982
V okolju, kjer nastopa velika gravitacija, tam prostor (razdalje) in čas zaznavamo
spremenjeno, kot to omejnja teorija relativnosti. Meter ni več meter ampak meter
s črtico (m'). Tudi sekunda ni več sekunda ampak (s').
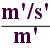V enačbi, ki določa frekvenco fotona ( f = c/l ) si ogledam merske enote.
Razdalja (m') v močnem gravitacijskem polju, kakršna koli že je, se v enačbi
krajša in ne vpliva na frekvenco fotona.
Na spremembo frekvence pa vpliva spremenjena hitrosti poteka časa (s'), kot
posledica velike gravitacije, v katerem nastane foton.
Gravitacija spremeni frekvenco izsevanega fotona.
Dogajanja v aktivnem galaktičnem središču je možno pojasniti ob predpostavki,
da se frekvenca izsevanih fotonov v črni luknji ali aktivnem galaktičnem središču
zmanjša kot posledica velike gravitacije za določen faktor.
Fotoni izsevani iz vodika v aktivnem galaktičnem središču ali v črni luknji
ob zapisani predpostavki še vedno kažejo značilen spekter vodikovih atomov le
na za določen faktor zmanjšani frekvenci.
Foton iz aktivnega galaktičnega središča ob navedeni predpostavki doživi rdeči
premik kot vsoto delovanja dveh zakonitosti:
· Hubblovega zakona o hitrosti in oddaljenosti aktivnega galaktičnega središča
· Spremembi frekvence fotona na izvoru zaradi velike gravitacije na aktivnem
galaktičnem središču.
S fizikalnimi meritvami učinkov ne moremo ločeno meriti. Merimo lahko le njun
skupni učinek.
Aktivna galaktična središča so pomešana med ostale galaksije.
Aktivna galaktična središča se od črnih lukenj razlikujejo v tem, da imajo
manjšo maso od črnih lukenj, toliko manjšo, da ne morejo zadržati izsevane svetlobe.
Aktivna galaktična središča niso niti tako masivna, niti tako oddaljena, niti tako hitra, kot bi lahko napačno sklepali le na osnovi Hubblovega zakona.
V črni luknji se foton posuši
Če v primeru aktivnega galaktičnega središča foton ali številčno osiromašen
grozd fotonov lahko pobegne iz galaksije, v primeru črne luknje tudi poslednji
foton iz grozda fotonov nima dovolj notranje (valovne) energije za osvoboditev
iz črne luknje.
Foton, ko ostane osamljen, ob dvigovanju iz črne luknje izgublja energijo.
Nekje na poti se dogodi, da foton ostane brez energije. Njegova valovna energija
postane enaka nič. Foton več ne obstaja.
Ob nastanku imajo fotoni grozda neko energijo v obliki elektromagnetnega valovanja,
obenem pa so ujeti v črni luknji. Grozd fotonov se nahaja v energijski kotanji
(črni luknji), zato je njegova izhodiščna potencialna energija negativna. Fotoni
so energijsko zadolženi.
Foton z dvigovanjem iz črne luknje poravna svoj energijski
dolg.
Grozdu fotonov se z dvigovanjem iz črne luknje povečuje njegova potencialna
energija, to pomeni, da se mu zmanjšuje njegov energijski dolg.
Zmanjševanje energije grozda fotonov se odraža v zmanjševanju števila fotonov
znotraj grozda na način, kot to prikazuje slika 7.2.
Potencialna energija grozda fotonov se povečuje v enakem obsegu, kot se grozdu
fotonov zmanjšuje energija (število) fotonov.
Ko na koncu ostane en sam foton, se potencialna energija fotona še naprej povečuje
in sicer v enakem obsegu, kot se fotonu zmanjšuje energija (amplituda) elektromagnetnega
valovanja.
Na koncu svoje poti ta osamljeni foton ne premore več nobene elektromagnetne
energije, vso energijo je porabil za dvigovanje, to je povečevanje lastne potencialne
energije v smeri od negativnih energijskih vrednosti proti energiji nič.
Ugotovim, da tudi ta poslednji foton po končanem dvigovanju ne obstaja več.
Nič ne ostane od njega. Ne obstaja njegova elektromagnetna energija in ne obstaja
njegova potencialna energija.
Najprej se zmanjšuje število fotonov v grozdu. Nato se izniči, "izhlapi"
še zadnji foton iz grozda.
Črne luknje rastejo in se krčijo.
Črna luknja nase privlači snovne delce in s tem se povečuje njena masa. Povečuje
se tako energija, kot tudi energijski dolg v obliki potencialne energije, ki
nastane pri padcu delca v črno luknjo.
Po zgledu že opisanega poskusa o padcu meteorita na sliki 2.1 (Energija), se
ob padcu snovnega delca v črno luknjo ustvari toplota in ustvari se energijski
dolg v obliki potencialne energije.
Obraten proces se dogaja pri sevanju fotonov. Za nastajanje in sevanje fotonov
črna luknja uporabi del lastne energije.
Po izničenju fotonov ob poskusu pobega in osvoboditve fotonov iz črne luknje,
črna luknja ostane brez dela svoje energije, tistega dela energije, ki ga črna
luknja porabi, za nastajanje izsevanih fotonov.
Sušenje črne luknje
Na ta način se črna luknja zmanjšuje in izginja. Izničevanje izsevanih fotonov
zmanjšuje maso črne luknje.
Če črna luknja za sevanje fotonov porabi več energije, kot jo pridobi s privlačenjem
snovnih delcev, potem se velikost in masa črna luknja zmanjšuje. V nasprotnem
primeru se masa črne luknje povečuje.
Črne luknje oziroma aktivna galaktična jedra rastejo in se sušijo. Črna luknja lahko preide v aktivno galaktično jedro, če se ji masa zaradi sevanja fotonov dovolj zmanjša, oziroma aktivno galaktično jedro se lahko spremeni v črno luknjo, če pritegne dovolj mase iz svoje okolice.
Črne luknje niso povsem črne.
Ko fotoni krožijo po vesolju, ali po zraku okrog nas, se med seboj 'zaletavajo'.
Zaletavajo pravzaprav ni pravi izraz, ker se ne zaletijo ampak preletijo drug
skozi drugega, kot je opisano v poglavju Foton.
Bližnja srečanja fotonov v naši okolici se dogodijo brez
posledic.
Če sedim na morski obali in ob razmerah z dobro vidljivostjo v opoldanskem
soncu opazujem ladjo daleč na morju, je vsak foton, ki vodoravno preleti razdaljo
od ladje do mojega očesa lahko 'prestreljen' z mnogimi fotoni, ki navpično letijo
od Sonca proti vodni gladini. Ta srečanja fotonov mi ne zmanjšujejo vidljivosti,
niti ne popačijo slike ladje.
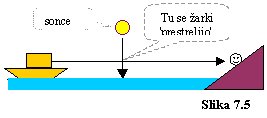
Opisana bližnja srečanja fotonov so opisana za razmere v naši okolici, na primer
na Zemlji. V nadaljevanju skušam sklepati, kako podobna bližnja srečanja fotonov
izgledajo v bližini črne luknje.
V črni luknji se fotoni dvignejo do iste višine.
Fotoni v izbrani črni luknji so podvrženi enaki gravitaciji pri poskusu pobega
iz črne luknje. Enaka začetna energija fotonov in enaka gravitacija pomeni,
da se vsi fotoni dvignejo do enake višine, preden se izničijo (izhlapijo).
V energijskem smislu niti ni pomembno, kako se fotoni povezujejo v grozde.
Vsak foton ima določeno energijo. Na vsak foton gravitacija deluje z določeno
silo, kar pomeni, da se da se zadnji fotoni grozda dvignejo do enake višine.
V črni luknji na ta način torej noben foton ne more zapustiti črne luknje.
To sklepanje pa ne potrjujejo opažanja. Fiziki opažajo, da črne luknje niso
povsem črne, da črne luknje deloma sevajo. To sevanje imenujemoHawkingovo sevanje
po fiziku Stephenu Hawkingu.
Optimalna energija fotona
Na izvoru vedno enaka energija fotona določene frekvence pomeni, da pri fotonu
obstaja neko optimalno energijsko stanje, vezano na frekvenco fotona.
Zmanjšanje energije zaradi energijskih izgub ob premagovanju gravitacije privede
foton v neko fotonu vsiljeno energijsko stanje. Foton preide v energijsko podhranjenost,
energijsko osiromašenje.
Pri posameznem fotonu je takšno osiromašenje lahko veliko, kadar pa fotoni
nastopajo v velikih grozdih, pa je takšno osiromašenje manj izrazito.
Nekaj podobnega se dogaja tudi s fotoni, ki iz okolice padajo v črno luknjo.
Črna luknja te fotone privlači. Privlačneje fotonov na neki poti (sila krat
pot) pomeni povečevanje energije padajočih fotonov.
Fotoni, ki padajo iz okolice v črno luknjo, so energijsko bolj bogati. Preveliko
energija se izraža v nastajanju novih fotonov znotraj grozda in povečevanje
števila fotonov znotraj istega grozda.
Srečevanje fotonov v gravitacijskem polju črne luknje.
Kadar se 'prestrelita' dva grozda fotonov z optimalno energijo in podobnim številom fotonov v grozdu, nimata večjega vpliva drug na drugega.
Fazna usklajenost fotonov lahko pomeni izmenjavo fotonov med grozdi fotonov,
kot prikazuje slika 3.17 v poglavju Foton.
Grozda fotonov praviloma svojo pot nadaljujeta, kot da drug za drugega ne obstajata.
V gravitacijskem polju črne luknje, na neki višini od površja črne luknje,
praviloma ni fotonov z optimalnim razmerjem med frekvenco in energijo fotona
(valovno dolžino in amplitudo valovanja).
Fotoni, ki zapuščajo črno luknjo so praviloma energijsko siromašni, v majhnih
grozdih. Pri dvigovanju izgubijo energijo in fotone grozda.
Grozdi fotonov, ki iz okolice padajo v črno luknjo, so po fotonih številčni
in energijsko bogati.
Osiromašeni fotoni težijo v optimalnejše energijsko stanje. V svoji okolici
iščejo manjkajočo energijo. Težijo k pridobitvi manjkajoče energije.
Podobno se dogaja tudi iz okolice padajočim fotonom v črno luknjo. So energijsko
preveč bogati in iščejo priložnost, da bi del svoje energije oddali in se na
ta način vrnili v optimalnejše energijsko stanje.
Srečanje fotonov se dogodi na način, kot to prikazuje slika 3.17 v poglavju Foton. Osiromašeni grozdi fotonov se številčno in energijsko obogatijo, številčno bogati grozdi fotonov pa ob predaji energije šibkejšim oslabijo.
Ne bojim se priznati nobene nasprotne zamisli, ker pričakujem, da bo prav od tam prišla resnica, ki je še ne poznam.
W. M. Pepper
Privilegiranim fotonom uspe pobeg iz črne luknje.
Kadar se na ustrezen način, tudi fazno usklajeno, kot je opisano v poglavju
Foton, 'prestrelita' energijsko siromašen grozd fotonov, dvigajoč se iz črne
luknje, z energijsko preveč bogatim in številčnim grozdov fotonov, padajočim
v črno luknjo, se obema hkrati ponudi priložnost za prehod v optimalnejše energijsko
stanje. Številčen grozd fotonov del fotonov preda številčno maloštevilnemu grozdu
fotonov.
Izmenjava se seveda lahko dogodi tudi na nivoju posameznega fotona. Grozd fotonov
lahko pomembno energijsko ojači energijsko siromašnemu fotonu.
Na ta način se dvigajoči in padajoči foton približata k optimalnemu energijskemu
stanju, to je energijskemu stanju, ki sta ga fotona imela v izhodišču.
Foton, ki se dviguje iz črne luknje s tem pridobi novo energijo. Tako pridobljena
energija pa mu mogoče že zadošča za pobeg iz črne luknje.
Črne luknje imajo različno svetilnost.
Koliko svetlobe pobegne iz črne luknje je torej odvisno, kolikšna je gravitacija
črne luknje, to je, koliko energije grozdu fotonov v izhodišču manjka, da bi
premagal gravitacijo črne luknje.
Po drugi strani je sevanje črne luknje odvisno tudi od tega kako svetla je
okolica črne luknje. Od svetlosti v okolici črne luknje je odvisna pogostost
vpada fotonov v črno luknjo, s tem pa verjetnost, da ima nek foton na pobegu
iz črne luknje privilegij, da se sreča z energijsko bogatim po frekvenci in
fazi sorodnim fotonom.
Za vrnitev v običajni format kliknite tukaj:
www.pozitivke.net
http://www.pozitivke.net/article.php/20050723141721675
|
|
| Domov |
|
Powered By GeekLog |
