| 
Vase sklenjeno energijsko
nihanje ustvari snov in snovi pripadajočo maso.
Einstein ugotavlja, da se energija lahko pojavi v obliki mase. Masa je po Einsteinu
oblika energije. Masa po Einsteinu vsebuje E= mc2 količino energije.
Prejšnje poglavje govori o vezalnih energiji, ki soustvarja snovne delce. Vezalna
energija je negativna oblika energije, je antienergija.
Vezalne energije in ujetosti snovnih gradnikov se na primer dogajajo na nivoju
majhnih delcev. Elektron je ujetnik atoma. Protone in nevtrone vezalna energija
povezuje v atomsko jedro. Kvarki so na podoben način povezani v protone in nevtrone.
Tudi planete vezalna energija povezuje s Soncem. Planeti so ujetniki Sonca,
sončni sistem je ujetnik galaksije.
Masa pomeni ujeto energijo in antienergijo.
Ko razmišljam o Einsteinovi enačbi E= mc2 moram torej razmišljati o energiji,
ki jo vsebuje masni delček, pa tudi o vezalni energiji to je negativni energiji
tega masnega delčka.
Zlom prostora je razpad "niča" v maso (energijo
in antienergijo)
Razmišljanje o prepletanju energije in antienergije v masnem delčku naj začnem
na nivoju najmanjših snovnih delcev.
Albrecht Giese je opisal fizikalni pojav, ki ga imenuje zlom prostora in pojasnjuje,
kako iz praznega prostora nastajajo masni delci.
Pri zlomu prostora iz praznega prostora, prostora ki pred zlomom ne vsebujejo
niti mase niti energije, nastaja energija in negativna energija (antienergija).
Energija in antienergija skupaj ustvarita energijsko tvorbo, ki jo opažamo v
obliki snovi.
Nihče, ki ni dovolil, da bi se smejali
na njegov račun, se še ni proslavil.
Marie Edgeworth
Kvark
 Domnevno matematično predstavo o omenjenem zlomu prostora nudi tudi porajajoča
se teorija strun. Najmanjše do sedaj poznane delce (kvarke) po teoriji strun
lahko razumemo kot energijske vrtince ali energijske vozle, zgolj kot vozlanje
energijskega in antienergijskega polja. Domnevno matematično predstavo o omenjenem zlomu prostora nudi tudi porajajoča
se teorija strun. Najmanjše do sedaj poznane delce (kvarke) po teoriji strun
lahko razumemo kot energijske vrtince ali energijske vozle, zgolj kot vozlanje
energijskega in antienergijskega polja.
Ko prehajamo k vse manjšim in manjšim snovnim tvorbam, ni nujno, da v vsaki
tvorbi kot gradnik neke snovne tvorbe nastopa snovni delec, na primer elektron,
ki se veže na atomsko jedro.
Pri najmanjših delcih, se lahko dogodi, da se preprosto med seboj zavozlata
energijsko in antienergijsko polje, tako kot prikazuje slika 5.1
Zasuk energijske ravnine
Kaj se dogaja na nivoju najmanjših delcev ni merljivo, zato si predstavo o
dogajanju skušam ustvariti na različnih modelih.
Enega od načinov predstave o zlomu prostora si lahko zamslim na način, ki ga
prikazuje slika 4.3 (Antienergija). Predstavljam si, da se del energijske ravnine
na sliki 4.3 vrti okrog osi x in s tem povzroči nihanje energije in antienergije
v neki izbrani točki, na primer na način, kot to kaže slika 5.1.
Načini interpretacije najmanjšega snovnega delca so lahko naslednji:
· model, ki si ga je zamislil Albrecht Giese,
· model energijskega in antienergijskega vozla prikazan na sliki 5.1 ali
· model kroženja dela energijske ravnine na sliki 4.3
Vsi navedeni modeli prikazujejo energijsko navezo energije in antienergije.
Povezana energije in antienergije v skupni vozel pomeni tako medsebojno povezavo,
da se ne energija in antienergija ne moreta ločiti. Tak skupni vozel lahko predstavlja
osnovni snovni delček.
Energijsko-antienergijske singularnosti
V nadaljevanju me zanima količina energije in antienergije v takem, prostorsko
zaokroženem energijskem vozlu oziroma nihanju, ki ga opazim kot snovni delček.
Ko se energijsko-antienergijski vozli, ki ustvarjajo snovni delček, povežejo
v večje snovne oblike, kvarki v nukleone, nukleoni v atomska jedra itd, dobimo
energijsko-antienergijske vozle bolj kompleksnih oblik.
Dobimo atome, molekule, snovne delce, planete, galaksije. Še vedno so to energijsko-antienergijski
vozli raznih oblik, kompleksnosti in velikosti.
Shemo energijskega vozla na sliki 5.1 lahko uporabim tako na nivoju kvarkov,
protonov in nevtronov, atomskih jeder do galaksij, kadar me zanimajo predvsem
energijsko stanje neke snovne oblike, manj pa oblika.
Take tvorbe, take povezave energije in antienergije lahko razumem kot energijske
in antienergijske singularnosti v prostoru.
Najmanjši snovni delci
Ker je sistem povezovanja delcev iz gledišča energijskih zakonitosti podoben
na vseh nivojih povezovanja, ni pomembno, ali so kvarki najmanjši snovni delci
ali se zlom prostora dogodi mogoče še na manjših delcih, kot so kvarki.
Na nivoju najmanjših snovnih delcev je tak vozel le eden, sestavljen iz energijskih
in antienergijskih polj, na višjih nivojih, na nivoju atomov, molekul, snovnih
delcev, pa je v taki energijsko-antienergijski singularnosti povezujejo združenja
takih vozlov nižjih nivojev.
Vsak snovni delček vsebuje energijo in antienergijo.
Snov torej vsebuje energijo in antienergijo, ki jo opazimo v obliki vezalnih
energij.
Čeprav sta si pozitivna in negativna oblika energije (energija in antienergija)
v snovnih delcih zelo blizu, se ne zlijeta. Ves čas v atomu obstajata vsaka
za sebe, vsaka s svojimi lastnostmi, pojavnimi oblikami in načinom delovanja.
Energijske in antienergijske singularnosti, kot jih predstavljajo snovni delci,
v svoji okolici ustvarjajo energijsko polje, tako kot prikazuje slika 2.9 v
poglavju Energija.
Matematični model kakršne koli energijske singularnosti pokaže, da energija
zavzame minimalno energijsko vrednost tako, da okrog singularnosti ustvari energijsko
polje oblike, ki jo kaže slika 2.9.
V oklici snovnega delca torej lahko pričakujemo energijsko polje
kot posledico v snovi vsebovane energije in antienergijsko polje kot posledico
v snovi vsebovane vezalne energije.
Energija se v prostoru razporeja z omejeno hitrostjo
V miselnem poskusu masni delček pospešim. Pospešim delček okrog katerega glede
na predhodne ugotovitve pričakujem energijsko in antienergijsko polje.
 V izhodišču tak masni delček obdaja energijsko in antienenrgijsko polje v obliki
krogle. Ko masni delček sunem (pospešim), se energijsko in antienenrgijsko polje
masnega delca razpotegne, tako kot kaže slika 5.2. S pospeševanjem snovnega
delca, delček izmaknemo iz sredine njemu lastnega energijskega polja. V izhodišču tak masni delček obdaja energijsko in antienenrgijsko polje v obliki
krogle. Ko masni delček sunem (pospešim), se energijsko in antienenrgijsko polje
masnega delca razpotegne, tako kot kaže slika 5.2. S pospeševanjem snovnega
delca, delček izmaknemo iz sredine njemu lastnega energijskega polja.
Energijsko polje novi lokaciji snovnega delca torej ne sledi hipno.
Energijsko polje masni delček dohiti, ko masni delček neham pospeševati
in šele po nekem sicer kratkem času. Ko masni delček ne pospešuje energijsko
polje po določenem času ponovno dobi obliko krogle.
Odziv snovnega delčka na sunek
Energijsko polje se na odmik delčka (energijske singularnosti) iz središča
lastnega energijskega polja odzove na dva načina:
· Ustvari nasprotno silo, ki skuša delček ohraniti na začetni lokaciji, v središču
izhodiščnega energijskega polja.
· Sočasno se polje začne preoblikovati in slediti novi lokaciji delčka v smislu
minimalnega energijskega stanja.
Newton je ugotovil, da se masni delec upira pospeševanju s silo, ki je enaka
F=m.a. (sila je masa krat pospešek)
Enačba pove, da pri enakomernem premočrtnem gibanju energijsko polje masnega
delca zlahka sledi spremembam lokacije delčka, brez delovanja proti sile. Energijsko
polje se razpotegne pri pospešenem gibanju snovnega delca.
Centripetalna sila
Poseben primer pospešenega gibanja je kroženje mase. Centripetalna sila, ki
deluje na maso, je posledica stalnega radialnega pospeška tega delca, s tem
pa stalne izmaknjenosti masnega delca iz središča lastnega energijskega polja.
Starost ni odvisna od let. Leta nagubajo
kožo, pomanjkanje radovednosti pa dušo.
General Douglas McArthur
Energijsko in antienergijsko polji delujeta avtonomno.
Opazna sila, ki se upira pospeševanju neke mase izhaja iz energijskega in antienergijskega
polja tega delca.
Snovni delec je energijska in antienergijska singularnost in s tem izvor energijskega
in antienergijskega polja okrog delca, zato se postavi vprašanje, kako učinkujeta
enenrgijsko in antienenrgijsko polje drug na drugega. Hipotetično lahko predvidimo
naslednje možnosti njunega medsebojnega učinkovanja:
· Energijsko in antienenrgijsko polje sta lahko popolnoma avtonomna in med seboj
ne učinkujeta, ali
· energijsko in antienergijsko polje se med seboj izničujeta zaradi nasprotnih
usmerjenosti.
Znanost bo nekoč našla jasen odgovor na to vprašanje.
Moč opažene sile v primeru pospeševanja pa že danes daje prednost prvi varianti,
ki pravi: energijsko in antienergijsko polje snovnega delca obstaja avtonomno.
Vsako za sebe prispeva svoj del k ustvarjanju mase snovnega delčka.
Sila, potrebna za pospeševanje, ki je pokazatelj mase, je torej domnevno vsota
delovanja energijskega in antienergijskega polja.
Einstein v svoji enačbi E=mc2 ne omenja antienergije.
Vsaka sprememba energije ali antienergije v neki snovi torej pomeni spremembo
njene mase.
Če je masa rezultat v snovi vsebovane energije in antienergije, se pojavi vprašanje,
kako si v teh novih okoliščinah lahko predstavljamo Einsteinovo enačbo E=mc2.
Če je masa posledica skupnega delovanja (vsote) energijskega in antienergijskega
polja, izhajajočega iz mase snovi, potem tudi Einsteinovo enačbo lahko dopolnim
v obliki vsote absolutnih vrednosti energije in antienergije: abs(Ep) + abs(En)
= mc2, kjer Ep pomeni absolutno vrednost pozitivne oblike energije v opazovani
snovi, En pa absolutno vrednost antienergije.
Energija E v Einsteinovi enačbi lahko predstavlja torej vsoto absolutnih vrednosti
količin v snovi vsebovane energije in antienergije.
Primarni vesoljski delci
Razmišljanje o energiji in antienergiji snovnega delčka je lahko dokaj akademsko
razmišljanje, lahko pa nam daje odgovore na še nerešena fizikalna vprašanja.
Fizika ima namreč še kar nekaj nepojasnjenih fizikalnih ugank.
Prof. dr. Janez Strnad v članku "Kdo bo spodnesel teorijo relativnosti"
omenja vstopanje zelo hitrih delcev v našo atmosfero. Te delce imenuje primarni
vesoljski delci.
Primarni vesoljski delci so atomska jedra, predvsem vodikova jedra, ki v našo
atmosfero vstopajo z izredno veliko hitrostjo in s tem z zelo veliko kinetične
energije.
Delci, čeprav so to masno zelo majhni delci, naj bi po opažanjih fizikov imeli
takšno energijo, kot če bi kilogramsko utež spustili z metra višine ali celo
višje.
Nikdar naj vas ne bo strah imeti lastnega
mnenja. Začrtajte si pot in se je držite. To je vse.
A.C.W. Harmsworth
V Argentini obstaja observatorij "Pierre Auger". ki že več let spremlja
vstopanje primarnih vesoljskih delcev v našo atmosfero.
V vrhnjih plasteh ozračja primarni vesoljski delci z veliko hitrostjo in energijo
udarijo v atome zraka (kisika, dušika) in s tem povzročijo plaz sekundarnih
vesoljskih delcev.
Količina vpadne energija primarnih vesoljskih delcev je nepredstavljiva.
Energijo, ki naj bi jo imeli ti primarni vesoljski delci je tako velika, da
jo je težko utemeljevati. Ni pojasnila, kako bi delci takšno hitrost in takšno
energijo sploh lahko dosegli. Če pa bi jo nekje na nek nepojasnjen način kljub
vsemu le dosegli, pa ni pojasnila, kako bi to neznansko veliko hitrost in energijo
na daljših razdaljah na poti proti Zemlji lahko zadržali.
Del opažene energije prinaša delček s seboj, del energije
pa delec pridobi pri trku ob atome v zraku.
Energija, ki jo opazimo in izmerimo ob vpadu hitrega delca, je izmerjena. O
izmerjeni količini energije ob padcu hitrega delca torej ni dvoma.
S tem pa ni nujno, da vso izmerjeno količino energije delec prinaša s seboj
iz vesolja. Dopustiti moramo možnost, da del energije delček prinese s seboj,
del energije pa si hitri delček pridobi kasneje v procesu trkanja delca v težje
atome zraka.
Pri velikem pospešku se atomsko jedro izmakne iz središča
lastnega energijskega polja.
Snovni delec, ki predstavlja energijsko singularnost, se izmakne iz središča
njemu lastnega energijskega polja, kadar ga pospešimo, tako kot prikazuje slika
5.2 na začetku tega poglavja.

Jedro energijske singularnosti, na primer atomsko jedro vodika, se lahko bolj
ali manj izmakne iz središča njemu lastnega energijskega polja, kot kaže slika
5.3.
Pri manjših pospeških snovnega delca je odmik delca iz središča njegovega lastnega
energijskega polja manjši kot pri velikih pospeških.
Masa snovi je odvisna od pospeška.
S kakšno silo energijsko polje deluje na snovni delec, je odvisno od tega,
kako tesno je snovni delec v stiku s svojim energijskim poljem.
Če je snovni delec približno v središču lastnega energijskega polja, potem
silo, ki deluje na delec določa Newtonov zakon F=m.a.
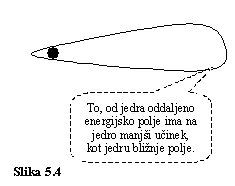
Kadar pa se delec (atomsko jedro vodika) zaradi velikih pospeškov bolj oddalji
od lastnega energijskega polja, kot to kaže slika 5.4, pa to oddaljeno polje
na delec deluje manj učinkovito, kot v primeru, kadar je delec v neposrednem
stiku z lastnim energijskim poljem.
Delec na nek način pobegne lastnemu energijskemu polju.
Vpliva energijskega polja, ki pripada masnemu delcu, na oviranje pospeševanja
masnega delca označujemo kot njegovo maso.
m = F/a
Masa snovi je torej kazalnik, s kakšno silo moramo delovati na nek delec, da
mu vsilimo določen pospešek.
Ko pospeški delcev postanejo veliki se delček vse težje brani
pred pospeški.
Pri velikih pospeških ima obkrožajoče polje delca zaradi popačitve, prikazane
na sliki 5.4 manjši vpliv na oviranje pospeševanja tega delca, kot pri manjših
pospeških.
Pri velikih pospeških se delec vse teže brani pospeškov.
To zmanjšano sposobnost oviranja pospeševanja s strani njemu lastnega energijskega
polja lahko izrazimo, kot zmanjševanje mase snovnega delca v času velikih pospeškov,
kot odvisnost mase masnega delca od lastnega pospeška.
To ugotovitev lahko zapišemo tudi v dopolnjenem Newtonovem zakonu, ki se v
dopolnjeni obliki glasi:
F
Sila, ki je potrebna za pospeševanje nekega delca je manjša ali enaka produktu
mase delca pri majhnih hitrostih in pospeška. Ne enačaj postane aktualen pri
velikih pospeških.
Vodikovo jedro se lahko odbije na različne načine.
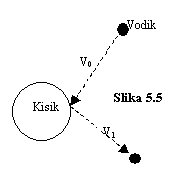 Ko na primer lahko vodikovo jedro na sliki 5.5 z veliko hitrostjo prileti iz
vesolja in se zaleti v precej težje jedro kisikovega atoma, je ta trk lahko
močan, lahko pa se jedri le oplazita. Ko na primer lahko vodikovo jedro na sliki 5.5 z veliko hitrostjo prileti iz
vesolja in se zaleti v precej težje jedro kisikovega atoma, je ta trk lahko
močan, lahko pa se jedri le oplazita.
Kadar se atoma le neznatno oplazita, takrat ne pride do velikih pospeškov.
Ta oblika trka je za nadaljnje razmišljanje manj zanimiva.
Za nadaljnje razmišljanje je zanimiv trk, ko se hitro vodikovo jedro v kisikovo
(ali dušikovo) jedro zaleti pod takim kotom, da pride do velikih pospeškov vodikovega
jedra.
Pri odboju hitrega vodikovega jedra od kisikovega jedra so pospeški lahko tako
veliki, da se energijsko polje hitrega vodikovega jedra zelo oddalji od jedra.
Dve fazi trka.
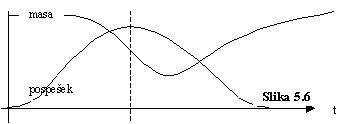
Da bi dogajanje ob trku jeder lažje razumel, trk časovno razdelim v fazo trka,
ko pospešek vodikovega jedra narašča in drugo fazo, ko se pospešek zmanjšuje.
Na sliki 5.6 oba dela trka ločuje črtkana črta na časovni osi.
V prvem delu trka, v času pred črtkano črto, je energijsko polje vodikovega
jedra dokaj urejeno ob jedru in še nepopačeno, kot kaže leva stran slike 5.3.
Skladnost energijskega polja okrog hitrega vodikovega jedra se učinkovito upira
pospeškom jedra.
V drugem delu trka, ko je energijsko polje hitrega vodikovega jedra vse bolj
razpotegnjeno in popačeno, kar prikazuje desna stran slike 5.3 oziroma slika
5.4. Takšno polje manj učinkovito brani jedro pred pospeški.
Manjšo sposobnost energijskega polja pri varovanju jedra pred pospeški lahko
razumem kot zmanjšanje mase vodikovega jedra v drugi fazi trka na sliki 5.6
v primeru velikih pospeškov.
Proti nejasni prihodnosti stopaj brez
strahu in možatega srca.
Henry Wadsworth Longfellow
Zmanjšanje mase kasni za maksimalnim pospeškom.
Zmanjšanje mase vodikovega jedra pri trku kasni za največjim pospeškom, tako
kot prikazuje diagram na sliki 5.6.
Jedro kisikovega atoma v drugem delu trka, ko je masa vodikovega atoma zmanjšana,
dokaj učinkovito z manjšim sunkom sile odrine vodikovo jedro.
Za kratek čas zmanjšana masa vodikovega jedra omogoča, da ga kisikovo jedro
odrine celo z večjo hitrostjo, kot je bila vpadna hitrost vodikovega jedra.
Trk
Ugotovitev je dokaj drzna, zato se ji posvetim s še nekaj razmišljanji.
Postavim se na mesto trka tako, da je energija, izhajajoča iz horizontalne
hitrosti prihajajočega vodikovega jedra enaka energiji z druge strani prihajajočega
kisikovega jedra.
 V tem sistemu opazovanja bi v okoliščinah brez velikih pospeškov lahko pričakoval
simetrični odboj. V tem sistemu opazovanja bi v okoliščinah brez velikih pospeškov lahko pričakoval
simetrični odboj.
Pri majhnih hitrostih in pospeških se vpadna hitrost obeh jeder po odboju ohranja,
v nasprotni smeri.
Ker vodikovo jedro v drugi fazi odboja nudi kisikovemu jedru nudi manjši odpor,
kot v prvi fazi odboja (pospeški za kratek čas vplivajo na maso vodikovega jedra)
je hitrost kisikovega jedra, prikazana na sliki 5.7, po odboju manjša od vpadne
hitrosti.
S tem se je hitrost in energija kisikovega jedra zmanjšala.
Hitrost vodikovega jedra pa se poveča zaradi začasno zmanjšanja mase vodikovega
jedra, kot to kaže slika 5.7.
Sunek sile
Opisano dogajanje si skušam ponazoriti na čim bolj razumljivem modelu, na primer
na takem, kot ga prikazuje slika 5.8.
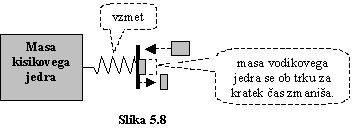
Slika prikazuje kisikovo in vodikovo jedro. Kisikovo jedro je zaradi večje
mase narisano večje. Elastičen trk si ponazorim z vzmetjo, v katero se zaleti
vodikovo jedro.
Ko vodikovo jedro zadane v kisikovo jedro, kinetični energiji njunega trka
prevzame vzmet.
Model na sliki 5.8 je najlažje predstavljiv, če sta v izhodišču energiji vodikovega
in kisikovega jedra enaki, kar pomeni, da po tem, ko pride do predaje njunih
kinetičnih energij vzmeti, se vodik in kisik za trenutek v celoti zaustavita.
V času napete vzmeti se vodikovemu jedru zaradi velikega pospeška zmanjša masa.
Učinek zmanjšanja mase je predvsem pri hitremu vodikovemu jedru, ki doživlja
mnogo večje pospeške kot pri počasnejšemu kisikovemu jedru.
V prvem delu trka sta obe masi še nezmanjšani, zato ustvarita masam primeren
sunek sile F.t. V drugi fazi trka se masa vodikovega jedra zmanjša, kar je na
sliki modela prikazano z manjšo površino ploskve, ki prikazuje vodikovo jedro.
Vzmet bo vso prejeto energijo vrnila vodikovemu in kisikovemu jedru, kar pomeni
enak sunek sile v fazi stiskanja vzmeti, kot v fazi raztezanja vzmeti.
Ker pa je v fazi odriva, vodikovo jedro brez dela svoje mase, ker se mu je
za hipec masa zmanjšala, ga bo vzmet odrinila z večjo hitrostjo, kot je bila
njegova vpadna hitrost. Hitrost kisikovemu jedru se bo zmanjšala glede na vpadno
hitrost, ker mu vodikovo jedro nudi manjši odpor.
Energijsko stanje
Dogodi se asimetrični odboj, kjer ob odboju več energije prevzame vodikovo
jedro, ki se mu zato hitrost poveča, manj energije pa kisikovo jedro, ki se
mu hitrost zmanjša glede na hitrosti pred odbojem.
Po trku se kisikovo jedro upočasni, zato prevzame manj energije, kot jo je
imel pred trkom.
Tudi vodikovo jedro je deležno manjšega sunka sile, vendar že manjši sunek sile
zagotovi večjo hitrost vodikovemu jedru po odboju zaradi trenutno zmanjšane
mase.
Energijska bilanca obeh jeder se kljub povečani hitrosti in energiji vodikovega
jedra ne spremeni.
Gibalna količina
Asimetričnost odboja pomeni spremembo gibalne količine sistema. Pri navedenem
elastičnem odboju se gibalna količina tradicionalno ne ohranja. Popačitve in
prerazporejanje enenrgijskih polj v primeru velikih pospeškov ne omogoča ohranjanje
gibalne količine sistema.
Padec hitrega primarnega vesoljskega delca ustvarja plaz
sekundarnih vesoljskih delcev.
Ugotovitev, da se vodikovemu jedru poveča energija ob trku s težjim atomskim
jedrom pa zahteva ponovno presojo o količini energije, ki jo s seboj prinašajo
primarni vesoljski delci iz vesolja.
Velika energija, ki jo opazimo ob vstopu teh delcev v naše ozračje v plazu
sekundarnih delcev nima izvora le v neznanski hitrosti delca pri vstopu, ampak
je posledica zaporednih trkov teh hitrih delcev v našem ozračju.
Primarni vesoljski delec mora seveda imeti zadostno hitrost in zadostno energijo,
da pospešek pri trku s težjim atomskim jedrom v ozračju uspe zadosti deformirati
energijsko polje takega delca.
Neuspeh ni napaka. Napaka je, če odnehamo.
B. F. Skiner
Koliko energije opazimo ob vstopu primarnega vesoljskega
delca je stvar naključja.
Če hitri vesoljski delec zadane v jedro atoma v ozračju tako, da se njegova
energija poveča in da s to povečano energijo delec naprej zadeva druge delce,
ki se ravno tako zaletavajo pod ugodnimi koti za povečevanje njihove energije,
to lahko sproži obsežen plaz sekundarnih vesoljskih delcev, ki dosežejo energijske
vrednosti, ki jih nikakor ne moremo pripisovati energijskemu stanju enega samega
vodikovega atomskega jedra.
Dogaja se nekaj podobnega, kot če spomladi na travniku zažgemo suho travo.
Pogori nekaj kvadratnih metrov trave, potem pa moramo postopek ponoviti. Energija
vžigalice ni pomembna za ogenj, ki se bo razvil. Če so ugodni pogoji lahko pride
do večjega požara, če teh pogojev ni potem ogenj hitro pogasne.
Podobno je pri vstopanju hitrih delcev v naše ozračje. Energija, ki se bo razvila
v sekundarnem plazu ni odvisna le od energije primarnega vesoljskega delca ampak
predvsem od naključij, kako bodo delci med seboj trkali.
Mora pa seveda primarni vesoljski delec imeti zadosti energije, da je s svojim
pospeškom sposoben sprožiti sekundarni plaz.
|